| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- lambda
- 분산시스템
- 병목
- Validation
- CHECK
- serverless
- fcm
- IaC
- rds
- PACELC
- Lamda
- sns
- kubernetes
- aws
- cloudwatch
- terraform
- SageMaker
- CAP
- amazonqcli
- Today
- Total
잡다한 IT 지식
프로그래머스 - 타겟 넘버 본문
본 알고리즘 풀이는 Routine Study에서 진행하고 있습니다.
저를 포함한 구성원이 대부분 초보이므로, 원하시는분은 언제라도 들어오셔도 좋습니다.
문의는 댓글 바람.
GitHub - ROUTINE-STUDY/Algorithm: 초보 알고리즘 스터디 / 누구나 참여 가능
초보 알고리즘 스터디 / 누구나 참여 가능 :runner:. Contribute to ROUTINE-STUDY/Algorithm development by creating an account on GitHub.
github.com
코딩테스트 연습 - 타겟 넘버
n개의 음이 아닌 정수가 있습니다. 이 수를 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다. -1+1+1+1+1 = 3 +1-1+1+1+
programmers.co.kr


[문제 설명]
- 각 숫자를 +,-할 수 있을 때 총합이 target이 되는 경우의 수
- 주의해야할 점 : 각 숫자는 1이상 50이하다. 무조건 1,-1이 아니다!
[처음 생각한 접근 방법]
1,-1이면 규칙이 있겠지만, 보니까 숫자가 1이상 50이하다.
그냥 무지성 모든 경우의 수를 해보는 수밖에 없어보인다.
예를 들어 주어진 수가 {1,2,3}이고 target이 6이다.
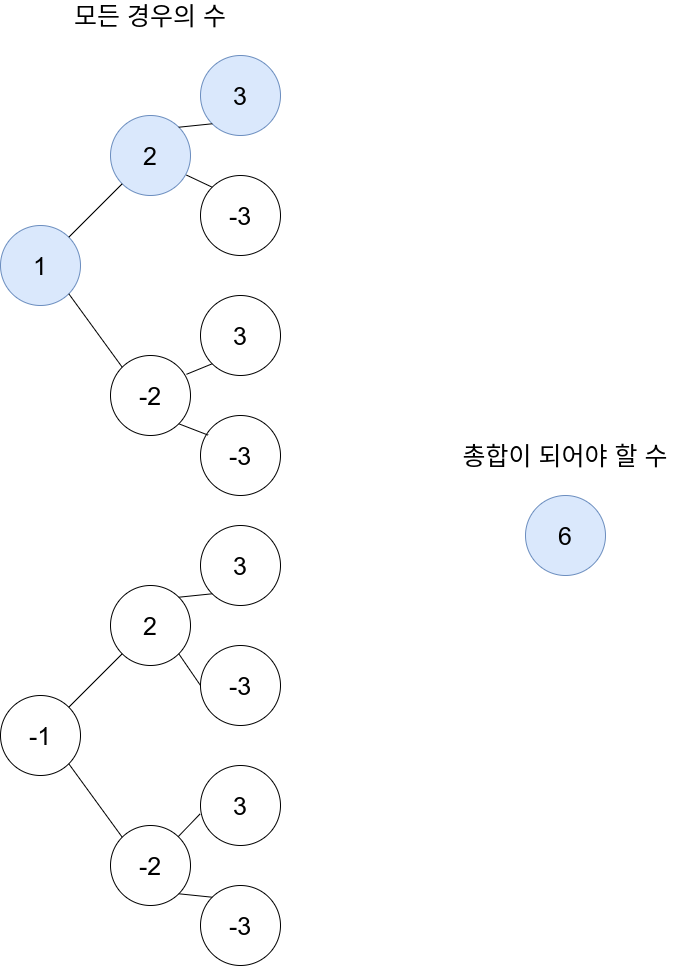
이런 식으로 모든 경우의 수를 돌면, 몇개가 일치하는지 알 수 있다. Stack을 활용한 DFS 방식으로 해도 됐을 문제 같다.
@@ -0,0 +1,18 @@
class Solution {
int answer = 0;
public int solution(int[] numbers, int target) {
recursion(numbers, 0, target);
return answer;
}
public void recursion(int[] numbers, int index, int target) {
if (index == numbers.length) {
if (target == 0) answer++;
return;
}
// 숫자를 + 로 주는 경우
recursion(numbers, index+1, target - numbers[index]);
// 숫자를 - 로 주는 경우
recursion(numbers, index+1, target + numbers[index]);
}
}+로 주는 경우 왜 target - numbers[index]가 되냐?
-> numbers = {1,2,3 }, target = 6이면
-> numbers의 첫번째 값이 +1이면 나머지 배열의 총합은 6-1인 5가 되면 된다. 즉, target은 target-numbers[index]
-로 주는 경우도 이와 마찬가지다.
-> numbers의 첫번째 값이 -1이면 나머지 배열의 총합은 6- (-1)인 즉, 7이 되야 한다. 결국 target은 target + numbers[index]
시간 복잡도는 메서드가 돌 때마다 2*2*2*.....2가 되므로 O(2^n)이 아닐까 싶다.
'알고리즘 문제 풀이 > DFS' 카테고리의 다른 글
| 백준 - 섬의 개수(Kotlin) (0) | 2022.02.23 |
|---|---|
| 백준 - 점프왕 쩰리 (못풀었다가 검토하다 다시 품) (0) | 2021.12.26 |
| 100. Same Tree (0) | 2021.08.10 |
| 94. Binary Tree Inorder Traversal (0) | 2021.08.09 |
| 589. N-ary Tree Preorder Traversal (0) | 2021.08.08 |


