| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 분산시스템
- IaC
- SageMaker
- lambda
- CAP
- cloudwatch
- CHECK
- serverless
- terraform
- rds
- Lamda
- 병목
- fcm
- Validation
- PACELC
- kubernetes
- amazonqcli
- aws
- sns
- Today
- Total
잡다한 IT 지식
백준 - 한동이는 공부가 하기 싫어!(Kotlin) 본문
본 알고리즘 풀이는 Routine Study에서 진행하고 있습니다.
https://github.com/ROUTINE-STUDY/Algorithm
저를 포함한 구성원이 대부분 초보이므로, 원하시는분은 언제라도 들어오셔도 좋습니다.
GitHub - ROUTINE-STUDY/Algorithm: 초보 알고리즘 스터디 / 누구나 참여 가능
초보 알고리즘 스터디 / 누구나 참여 가능 :runner:. Contribute to ROUTINE-STUDY/Algorithm development by creating an account on GitHub.
github.com
문의는 댓글 바람.
문제 출처 : https://www.acmicpc.net/problem/3182
[문제 설명]
어떤 선배한테 물어봐야 최대한 많은 선배를 만날 수 있을까?
주어진 선배들의 관계는 그래프. 그 중에서도 방향 그래프로 표현할 수 있다. (1번 선배가 2번 선배를 소개한다고 해도, 2번 선배는 1번 선배를 소개 안 할 수도 있기 때문이다.)
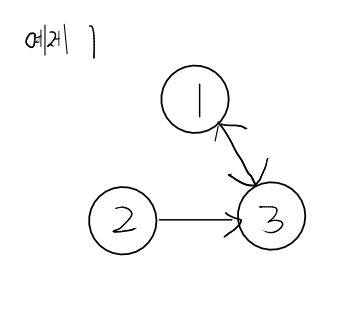
또한, (1번선배, 2번선배), (2번선배, 1번선배)와 같이 대칭 관계나 (1번,2번), (2번,3번), (3번,1번)처럼 사이클이 존재할 수도 있으므로 방문한 요소는 체크를 해주는 게 맞다.
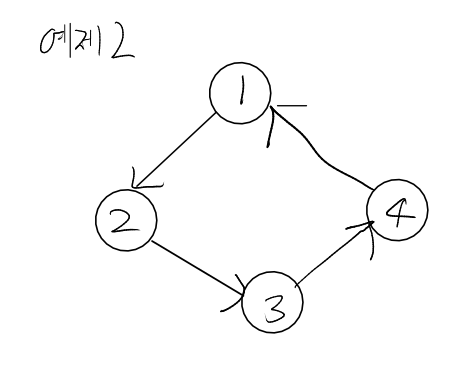
[코드를 짜기 전에 생각 정리]
1. 입력을 받는다.
2. 선배들의 관계를 리스트로 표현하는데 그래프의 차수가 모두 1이므로 List나 2차원 배열 등을 사용하지 않고 그냥 정수형 배열을 써준다. (만약 차수가 여러 개면 2차원 배열이나 List를 통해 모든 관계를 표현해야하지만, 차수가 1이면 필요 없다.)
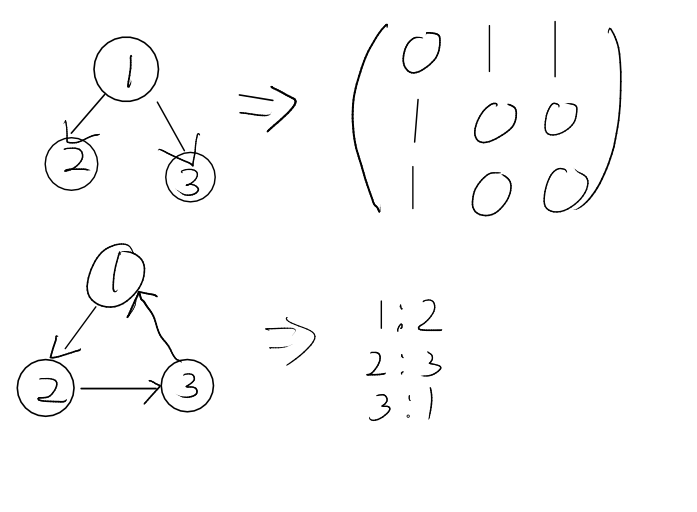
3. 그래프의 1,2,3,..,N번을 첫 시작점으로 잡고 그래프를 탐방한다. (방문여부 처리를 할 배열은 매번 새로 만들어야 한다. 다른 선배가 만났던 선배였는지는 상관 없으므로)
3-1. 현재 선택한 선배를 통해 만날 수 있는 사람이 지금까지 최대로 만난 선배수보다 많으면 선배의 번호와 만날 수 있는 사람의 수를 최신화한다. (조건으로 만날 수 있는 사람의 수가 같으면 작은 번호를 출력하라는데, 1번 선배부터 출력하므로 따로 조건을 걸어줄 필요가 없다.)
4. 모든 순서를 확인했으면 가장 많이 만날 수 있는 번호를 출력한다.
시간복잡도는 모든 선배가 최대한 많이 만난다고 가정했을 때 최악의 경우 O(N^2)이 될듯하다.
[Kotlin 코드]
import java.io.BufferedReader
import java.io.InputStreamReader
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
// 현재 최고 인맥 선배
var noOfBestElder = 0
// 현재 최고로 많이 만난 게 몇명인지
var maxPathLength = Int.MIN_VALUE
// 선배 인원수
val cntOfElder = readLine().toInt()
// 선배 번호는 1번부터 시작이므로 배열을 인원수보다 1 크게 만들어준다.
val relationship = IntArray(cntOfElder+1)
// 선배가 추천하는 선배를 입력해준다
// 인덱스 : 현재 선배의 번호, 값 : 현재 선배가 추천하는 다음 선배 번호
for (numOfElder in 1..cntOfElder) {
relationship[numOfElder] = readLine().toInt()
}
// 1~N번까지 번호를 시작점으로 잡고 최대 몇명을 만나는지 확인한다.
for (numOfElder in 1..cntOfElder) {
// 현재 선배를 통해 만나고 있는 사람 수
var currentPathLength = 1
val map = BooleanArray(cntOfElder+1)
// 현재 만나고 있는 선배 번호
var currentPosition = numOfElder
map[currentPosition] = true
// 만났던 선배면 반복문을 종료한다.
while (!map[relationship[currentPosition]]) {
// 만났던 선배가 아니므로 만난 선배 인원수가 추가됨.
currentPathLength++
// 만났다고 처리해줌.
map[relationship[currentPosition]] = true
// 다음 만날 선배가 이제 만나는 중인 선배가 됨.
currentPosition = relationship[currentPosition]
}
// 현재 선배를 통해 만날 수 있는 사람의 수가 이전 최고기록보다 높으면 갈아치움.
if (currentPathLength > maxPathLength) {
noOfBestElder = numOfElder
maxPathLength = currentPathLength
}
}
println(noOfBestElder)
}[느낀 점]
무지성 그래프라고 생각하고 풀었으면 2차원 배열이나 리스트를 이용해서 관계를 표현했겠지만 그러한 비용을 충분히 아낄 수 있는 문제다.
2차원 배열로 표현했으면 메모리가 O(N^2). 리스트로 표현했으면 N명의 선배가 1명씩 추천하므로 메모리가 O(N).
시간복잡도는 N명의 선배가 최대 N-1명의 선배를 만나므로 N*(N-1)이므로 O(N^2)이 될 듯하다.
'알고리즘 문제 풀이 > 그래프' 카테고리의 다른 글
| 백준 - 죽음의 게임(Kotlin) (0) | 2022.04.09 |
|---|---|
| 백준 - 태권왕(Kotlin) (0) | 2022.04.09 |
| 백준 - 미로 탐색(Kotlin) (0) | 2022.02.05 |
| 백준 - 유기농 배추(Kotlin) (0) | 2022.02.03 |
| 백준 - 상근이의 여행(Java) (0) | 2022.02.02 |
