| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- IaC
- kubernetes
- serverless
- aws
- VM
- 병목
- cloudwatch
- Lamda
- lambda
- amazonqcli
- CAP
- sns
- fortigate
- Validation
- fortinet
- terraform
- rds
- 분산시스템
- CHECK
- PACELC
- SageMaker
- Evaluation License
- fcm
- Today
- Total
잡다한 IT 지식
백준 - N번째 큰 수 본문
본 알고리즘 풀이는 Routine Study에서 진행하고 있습니다.
https://github.com/ROUTINE-STUDY/Algorithm
저를 포함한 구성원이 대부분 초보이므로, 원하시는분은 언제라도 들어오셔도 좋습니다.
GitHub - ROUTINE-STUDY/Algorithm: 초보 알고리즘 스터디 / 누구나 참여 가능
초보 알고리즘 스터디 / 누구나 참여 가능 :runner:. Contribute to ROUTINE-STUDY/Algorithm development by creating an account on GitHub.
github.com
문의는 댓글 바람.
문제 출처 : https://www.acmicpc.net/problem/2693
[문제 설명]
자연수로 이어진 배열이 주어졌을 때 n번째로 작은 수를 구하여라.
[접근 방법]
일단 주어진 문제를 먼저 보도록 하겠습니다.

배열의 크기는 10밖에 되지 않고 원소의 값은 1,000보다 작은 자연수입니다.
배열의 크기가 굉장히 작으므로 아무 생각하지 않고 퀵정렬한 후에 답을 구해도 됩니다.
그러나, 그보다 빨리 풀고 싶다면 선택 정렬을 이용한 분할 정복 방법을 사용하면 됩니다.
선택정렬을 이용하여 pivot의 마지막 위치의 값이 n보다 작으면 오른쪽을 분할 정복하고, pivot의 마지막 위치의 값이 n보다 크면 왼쪽을 분할 정복합니다.
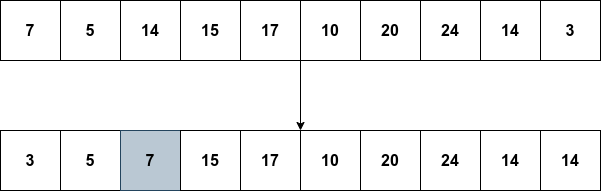
1차 정렬이 끝난 후에 7에 위치가 3이므로 8(3번째로 작은 수 위치)보다 작으므로
다음엔 위치 4부터 10까지에서 위 과정을 반복해줍니다.

시간복잡도는 배열이 정렬되어 있을 때 최악으로 O(배열의 길이^2), 평균은 O(배열의 길이)가 됩니다.
[코드]
import java.io.BufferedReader
import java.io.InputStreamReader
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val t = readLine().toInt()
val n = 7
repeat(t) {
val array = readLine().split(" ").map { it.toInt() }.toIntArray()
val answer = getNthNumber(n = n, array = array, left = 0, right = array.size - 1)
println(answer)
}
}
fun getNthNumber(n: Int, array: IntArray, left: Int, right: Int): Int {
var cLeft = left + 1
var cRight = right
if (left !in array.indices || right !in array.indices) {
return -1
}
while (cLeft <= cRight) {
while (cLeft < right && array[cLeft] <= array[left]) {
cLeft++
}
while (cRight > left && array[cRight] >= array[left]) {
cRight--
}
if (cLeft < cRight) {
array[cLeft] = array[cRight].also { array[cRight] = array[cLeft] }
} else {
array[left] = array[cRight].also { array[cRight] = array[left] }
return if (cRight < n) {
getNthNumber(n = n, array = array, left = cRight + 1, right = right)
} else if (cRight > n) {
getNthNumber(n = n, array = array, left = left, right = cRight - 1)
} else {
array[cRight]
}
}
}
return array[left]
}
[생각해볼것]
선택정렬을 간만에 구현하려니까 굉장히 헷갈렸습니다. 가끔 구현해보는 것도 좋을 듯 합니다.
만약, 배열의 크기가 훨씬 커진다면 계수정렬을 사용하는 것이 좋습니다.(원소의 값은 1,000보다 작은 자연수니까)
'알고리즘 문제 풀이 > 이분탐색' 카테고리의 다른 글
| 5207. 파이썬 SW 문제해결 구현 4일차 - 이진 탐색 (0) | 2025.04.29 |
|---|---|
| [LeetCode] - 35. Search Insert Position (0) | 2023.07.05 |
| 백준 - 공유기 설치(Kotlin) (0) | 2022.02.15 |
| 백준 - 랜선 자르기(Java) (0) | 2022.01.17 |
| 백준 - 숫자 카드 (0) | 2022.01.04 |


