Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- rds
- sns
- PACELC
- SageMaker
- Validation
- CAP
- fcm
- CHECK
- cloudwatch
- lambda
- aws
- kubernetes
- 분산시스템
- Lamda
- amazonqcli
- 병목
- terraform
- serverless
- IaC
Archives
- Today
- Total
잡다한 IT 지식
23005. 회문 만들기 본문
태그 잊지 않고 붙이세요
#Algorithm #bfs #D4 #Solved
문제 링크
제한사항
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스는 한 개의 줄로 구성되며, 각 줄에는 알파벳 소문자로만 구성된 문자열 S가 주어진다. S의 길이는 1 이상 100,000 이하이다.
문제 정리
- 문자 'x'를 넣어서 회문을 만들 수 있나?
회문을 만드는데 필요한 연산 횟수는 몇번인가?
접근 방법
회문이 되려면 간단히 시작과 끝이 같으면 된다.
두 문자가 같은 경우
만약, 두 문자가 같다면 다음 문자로 넘어가면 된다. 이를 반복한다.
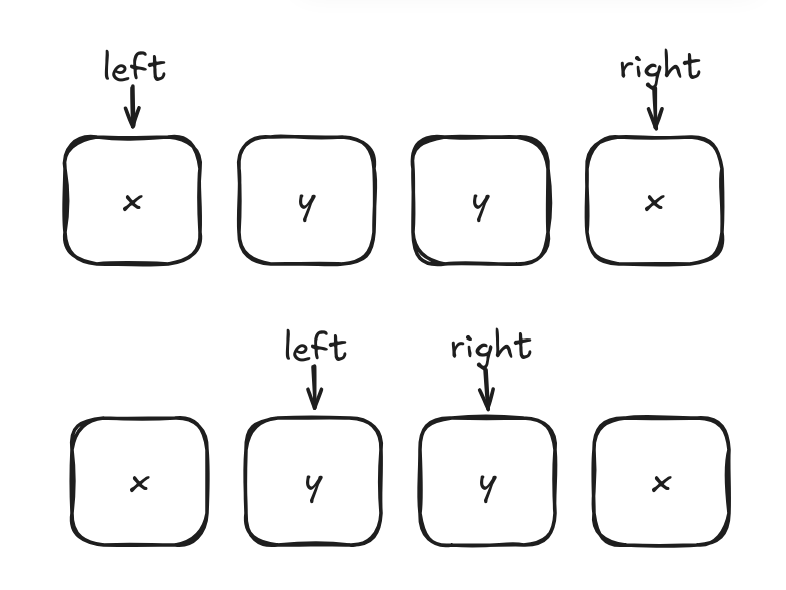
두 문자가 다른 경우
문자가 같은 경우는 생각했으므로 이제 문자가 서로 다른 경우를 생각하면 된다.
이 경우엔 2가지 분기로 나뉜다. 우선, 한 문자만 'x'일 경우다.

이럴 땐, 'x' 문자열을 넣을 수 있으므로 left 왼쪽에 x를 넣으면 된다. x를 넣으므로 연산 횟수가 1 증가한다.

연산 후엔 어떻게 될까? left는 그대로 두고 right를 왼쪽으로 옮긴다.

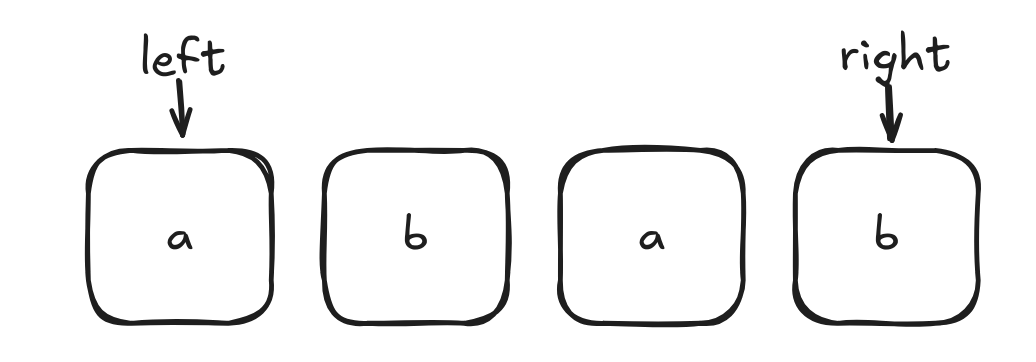
두 번째 케이스는 둘다 'x'가 아닌 경우다.
이 경우엔 회문이 될 수 없다. 우리가 할 수 있는 연산은 'x' 삽입만 가능하기 때문이다.
결론을 정리하자면 다음과 같다.
- left, right의 값이 같으면 각각 1칸씩 이동한다. 이 때, 삽입은 이뤄지지 않았으므로 연산 횟수는 증가하지 않는다.
- lefit, right의 값이 같지 않으면 케이스는 두 가지로 나뉜다.
- 한 쪽이 x라면 해당 포인터만 이동한다. 이 때, x가 삽입이 됐으므로 연산 횟수가 1 증가한다.
- 둘다 x가 아니라면 해당 문자열은 회문이 될 수 없다.
위에선 'x'를 넣는다고 말했지만 연산 횟수를 구하는 것이 목표이므로 실제로 'x'를 삽입하진 않는다.
포인터를 이동해주는 것으로 충분하다.
복잡도
시간복잡도: O(문자열 s의 길이)
공간복잡도: O(문자열 s의 길이)
코드
T = int(input())
def bfs(word):
queue = []
queue.append((0, len(word) - 1, 0))
while queue:
left, right, depth = queue.pop()
if left >= right:
return depth
l_char = word[left]
r_char = word[right]
if l_char == r_char:
queue.append((left + 1, right - 1, depth))
elif l_char != 'x' and r_char != 'x':
return -1
else:
if l_char == 'x':
queue.append((left + 1, right, depth + 1))
elif r_char == 'x':
queue.append((left, right - 1, depth + 1))
return -1
for test_case in range(1, T + 1):
word = input()
answer = bfs(word)
print(answer)
# print(f"#{test_case} {answer}")'알고리즘 문제 풀이 > 배열' 카테고리의 다른 글
| 프로그래머스 - 로또의 최고 순위와 최저 순위 (0) | 2021.11.17 |
|---|---|
| 1200. Minimum Absolute Difference (0) | 2021.09.13 |
| 1122. Relative Sort Array (0) | 2021.09.06 |
| 169. Majority Element (0) | 2021.07.03 |
| Find the Winner of the Circular Game (0) | 2021.04.11 |



