Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- Validation
- cloudwatch
- PACELC
- sns
- kubernetes
- terraform
- Lamda
- fcm
- amazonqcli
- CAP
- lambda
- rds
- 병목
- IaC
- SageMaker
- CHECK
- serverless
- 분산시스템
- aws
Archives
- Today
- Total
잡다한 IT 지식
BFS 본문
참고한 영상
BFS 위키백과
너비 우선 탐색(Depth-First Search)
너비 우선 탐색(Breadth-first search, BFS)은 맹목적 탐색방법의 하나로 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법이다.
큐를 이용해서 구현합니다.
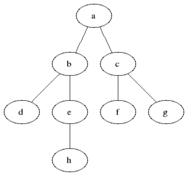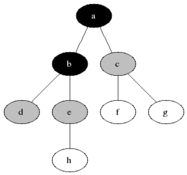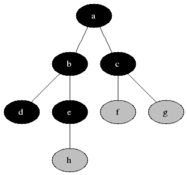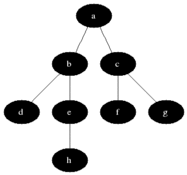
- 장점
출발노드에서 목표노드까지의 최단 길이 경로를 보장한다. - 단점
경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.
영상 보면서 직접 코틀린으로 구현해본 소스 코드.

import java.util.*
class Graph(val size : Int = 10) {
val nodes: Array<Node> = Array<Node>(10, { i -> (Node(i))})
class Node(var data : Int = 0, var adjacent : LinkedList<Node> = LinkedList(), var marked : Boolean = false)
fun addEdge(original : Int, adjacent : Int) { //인접 노드 설정하는 메소드.
val node1 = nodes[original]
val node2 = nodes[adjacent]
if (!node1.adjacent.contains(node2)) {
node1.adjacent.add(node2)
}
if (!node2.adjacent.contains(node1)) {
node2.adjacent.add(node1)
}
}
fun bfs() {
bfs(0)
}
fun bfs(index:Int) {
val queue : Queue<Node> = LinkedList<Node>()
when (nodes[0]) {
null -> return
else -> queue.offer(nodes[0])
}
nodes[0].marked = true
while (!queue.isEmpty()) {
val node = queue.poll()
for (ad in node.adjacent) {
if (ad.marked == false) {
ad.marked = true
queue.offer(ad)
}
}
println(node.data)
}
}
}
fun main() {
val graph : Graph = Graph(10)
graph.addEdge(0,1)
graph.addEdge(1,3)
graph.addEdge(1,4)
graph.addEdge(3,7)
graph.addEdge(3,8)
graph.addEdge(4,9)
graph.addEdge(0,2)
graph.addEdge(2,5)
graph.addEdge(2,6)
graph.bfs()
}'알고리즘 문제 풀이 > BFS' 카테고리의 다른 글
| 103. Binary Tree Zigzag Level Order Traversal (0) | 2021.07.22 |
|---|---|
| 559. Maximum Depth of N-ary Tree (0) | 2021.07.08 |
| 226. Invert Binary (0) | 2021.07.05 |
| 690. Employee Importance (0) | 2021.07.01 |
| 01 Matrix (0) | 2021.04.14 |




