Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- fcm
- cloudwatch
- Validation
- serverless
- terraform
- PACELC
- IaC
- aws
- sns
- 분산시스템
- CAP
- CHECK
- 병목
- lambda
- SageMaker
- rds
- kubernetes
- amazonqcli
- Lamda
Archives
- Today
- Total
잡다한 IT 지식
백준 - 숫자 정사각형(Kotlin) 본문
알고리즘 풀이는 Routine Study에서 진행하고 있습니다.
https://github.com/ROUTINE-STUDY/Algorithm
저를 포함한 구성원이 대부분 초보이므로, 원하시는분은 언제라도 들어오셔도 좋습니다.
GitHub - ROUTINE-STUDY/Algorithm: 초보 알고리즘 스터디 / 누구나 참여 가능
초보 알고리즘 스터디 / 누구나 참여 가능 :runner:. Contribute to ROUTINE-STUDY/Algorithm development by creating an account on GitHub.
github.com
문의는 댓글 바람.
문제 출처 :https://www.acmicpc.net/problem/2468
[문제 설명]
각 꼭지점의 값이 같은 최대 크기 정사각형을 구하시오.
[접근 방법]
완전탐색하는 수밖에 없다.
정사각형의 변의 최소 길이는 1이고 최대 길이는 N,M중에 작은 값.
변의 길이가 1인 정사각형부터 최댓값까지 모두 만들어보고 모든 좌표에서 체크하면 된다.
시간 복잡도는 정사각형의 길이를 K라고 뒀을 때, 좌표를 체크하는 횟수가 (N-K+1)(M-K+1)이다.
예를 들어, 정사각형의 길이가 2고 직사각형의 길이가 2*2라고 치자. (2-2+1)(2-2+1) = 1번만 체크하면 된다.
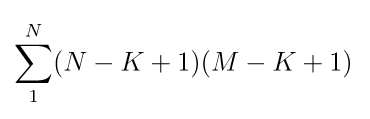
최악의 경우 N = M이라고 두고 수식을 단순화하면 시간복잡도는 O(N^3) 즉, 50^3 = 125,000이 된다.
따라서, 시간복잡도는 여유가 있다.
[코드]
import java.io.BufferedReader
import java.io.InputStreamReader
fun main() = with(BufferedReader(InputStreamReader(System.`in`))) {
val (N, M) = readLine().split(" ").map { it.toInt() }
// 정사각형의 최소 길이
val minLength = 1
// 정답
var answer = minLength * minLength
// 정사각형의 최대 길이
val maxLength = N.coerceAtLeast(M)
// 정사각형 지도
val square = Array(N) { IntArray(M) }
repeat(N) { rIdx ->
readLine().forEachIndexed { cIdx, value ->
square[rIdx][cIdx] = value.digitToInt()
}
}
for (length in maxLength downTo 1) {
for (rIdx in square.indices) {
for (cIdx in square[rIdx].indices) {
// 정사각형의 좌표를 벗어나면 continue
if (rIdx + length - 1 >= N || cIdx + length - 1 >= M) {
continue
}
// 정사각형의 네 점의 좌표의 값이 같으면 크기를 갱신해줌.
val pivot = square[rIdx][cIdx]
if (pivot == square[rIdx][cIdx + length - 1] &&
pivot == square[rIdx + length - 1][cIdx + length - 1] &&
pivot == square[rIdx + length - 1][cIdx]
) {
answer = length * length
println(answer)
return
}
}
}
}
println(-1)
}'알고리즘 문제 풀이 > 완전탐색' 카테고리의 다른 글
| 프로그래머스 - 양궁대회(Kotlin) (0) | 2022.11.14 |
|---|---|
| 백준 - N과 M(2) Kotlin (0) | 2022.07.19 |
| 백준 - 크면서 작은 수(Kotlin) (0) | 2022.04.19 |
| 백준 - 근손실(Kotlin) (0) | 2022.04.19 |
| 백준 - 치킨 배달(Kotlin) (0) | 2022.02.22 |

