| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- kubernetes
- IaC
- cloudwatch
- CHECK
- lambda
- sns
- SageMaker
- 병목
- fcm
- Lamda
- amazonqcli
- rds
- Validation
- terraform
- CAP
- PACELC
- 분산시스템
- aws
- serverless
- Today
- Total
잡다한 IT 지식
백준 - N과 M(2) Kotlin 본문
본 알고리즘 풀이는 Routine Study에서 진행하고 있습니다.
https://github.com/ROUTINE-STUDY/Algorithm
저를 포함한 구성원이 대부분 초보이므로, 원하시는분은 언제라도 들어오셔도 좋습니다.
GitHub - ROUTINE-STUDY/Algorithm: 초보 알고리즘 스터디 / 누구나 참여 가능
초보 알고리즘 스터디 / 누구나 참여 가능 :runner:. Contribute to ROUTINE-STUDY/Algorithm development by creating an account on GitHub.
github.com
문의는 댓글 바람.
문제 출처 :https://www.acmicpc.net/problem/15650
[문제 설명]
1부터 N까지의 자연수 중에 M개를 선택하여 차례대로 줄 세울 수 있는 경우를 모두 구하라.
[접근 방법]
모든 경우를 탐색하면 된다.
단, 배열의 남은 요소를 모두 선택해도 전체 수열의 크기가 M이 될 수 없다면 이는 불가능한 경우이므로 종료한다.
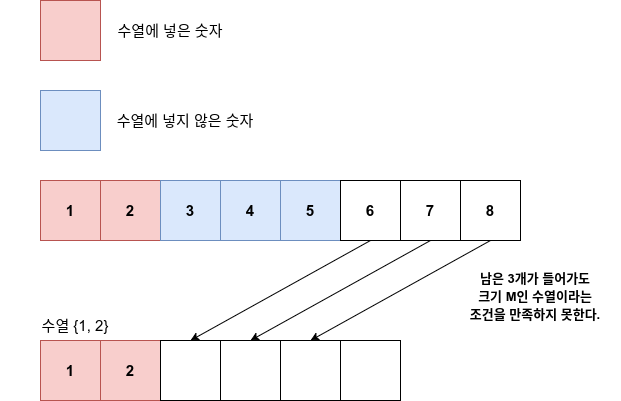
예 : 입력이 8 6일 때, 수열 {1, 2}가 있고 3, 4, 5를 넣지 않고 6을 넣을지 말지 고민하고 있다.
이 고민이 과연 필요할까? 필요 없다. 만약, 6을 넣고 나머지 든 요소를 넣어서 완성되는 배열은 {1, 2, 6, 7, 8}로 크기가 5밖에 되지 않아 M을 만족할 수 없다.
즉, 5를 넣지 않는 순간 과감하게 메서드를 종료해야 했던 것이다.
시간복잡도는 N*(N-1)*(N-2)*...*(N - M + 1)*(N - M) => O(N^M)이 된다.
import java.util.*
fun main() {
// 1 <= M <= N <= 8, N^N해도 시간적 여유가 있음(브루트 포스 가능)
// 중복 없이 고른 수열
// 오름차 순이어야 한다.
val (n, m) = readln().split(" ").map { it.toInt() }
println(getSequential(m, 0, sequence = LinkedList(), n))
}
// remainCnt : 남은 수열의 요소 개수
// prevNum : 이전 선택한 수열의 값 (1,3 -> 3이 이전 선택한 값)
// sequnce: 현재 수열의 상태
// n: 마지막 숫자
fun getSequential(remainCnt: Int, prevNum: Int, sequence: LinkedList<Int>, n: Int): StringBuilder {
val sb = StringBuilder()
// if : 남은 개수보다 남은 숫자가 적으면 끝
if (remainCnt > n - prevNum) {
return sb
} else if (remainCnt == 0) {
sequence.forEach {
sb.append("$it ")
}
sb.append("\n")
return sb
} else if (prevNum == n) {
return sb
}
for (i in prevNum + 1..n) {
sequence.add(i)
sb.append(getSequential(remainCnt - 1, prevNum = i, sequence, n))
sequence.removeLast()
}
return sb
}
'알고리즘 문제 풀이 > 완전탐색' 카테고리의 다른 글
| SWExpert Academy: 2001. 파리 퇴치 (0) | 2025.04.24 |
|---|---|
| 프로그래머스 - 양궁대회(Kotlin) (0) | 2022.11.14 |
| 백준 - 숫자 정사각형(Kotlin) (0) | 2022.04.21 |
| 백준 - 크면서 작은 수(Kotlin) (0) | 2022.04.19 |
| 백준 - 근손실(Kotlin) (0) | 2022.04.19 |

